个人计算机知识展示

Appearance

二分搜索 ​

https://docs.python.org/zh-cn/3/library/bisect.html

定义 ​

首先，假设表中元素是按升序排列，将表中间位置记录的关键字与查找关键字比较，如果两者相等，则查找成功；否则利用中间位置记录将表分成前、后两个子表，如果中间位置记录的关键字大于查找关键字，则进一步查找前一子表，否则进一步查找后一子表。重复以上过程，直到找到满足条件的记录，使查找成功，或直到子表不存在为止，此时查找不成功。

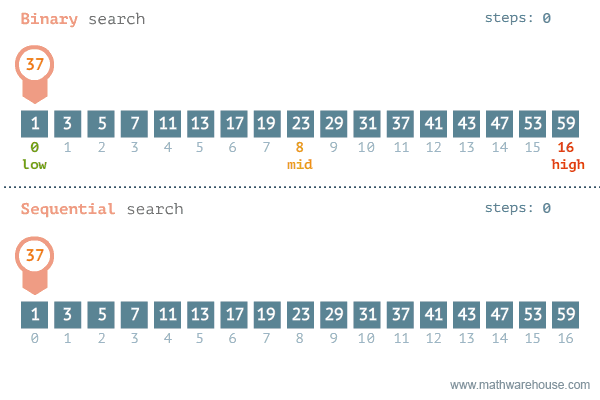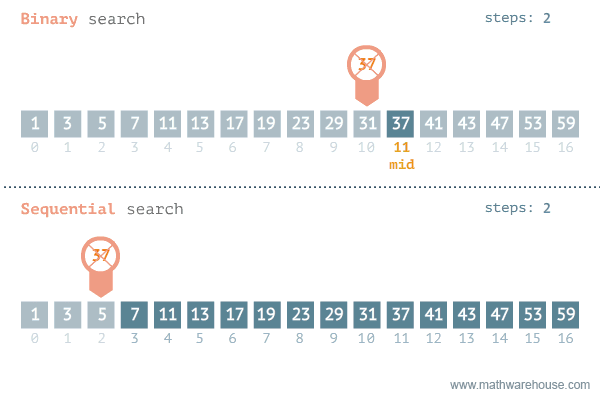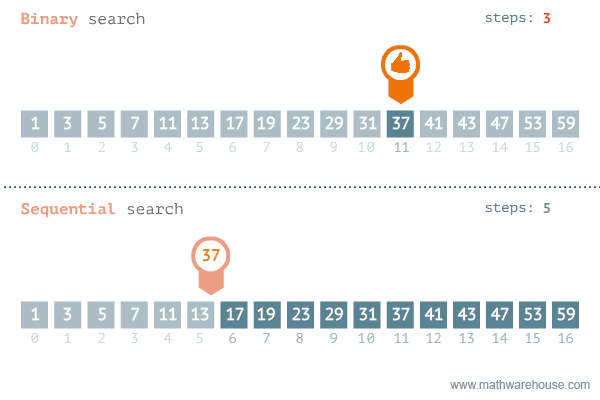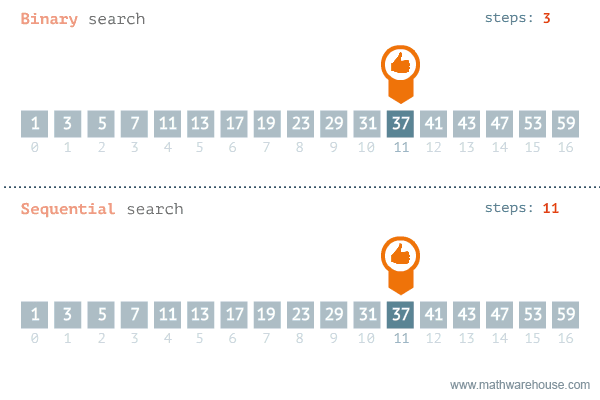
示例 ​

简单查找

假设现在有 1024 个有序的数字序列 numbers，数字大小范围在 0~10000 之间。如果我们要查找一个数字 target ，在不在 numbers 里面，请问最多要找多少次？

题目解析

如果不去思考，那么你可能最多要找 1024 次，但是如果会设计算法，那么最多只需要找 10 次（就是 log21024）。

假设 numbers 序列的长度的为 n，上面的问题如果选择从左到右逐一查找的话，属于线性搜索，最多要找 n 次。如果采用二分搜索的话，最多只需要查找 log2n次。

这里就体现出了设计一种高效算法的好处！

这个区别通过折线图 📈 可以进一步看出明显的效率提升。(X 轴代表 numbers 的数量，Y 轴代表搜索次数。)

那么，二分搜索究竟是怎么实现的呢？请继续往下看。

二分搜索算法主要有三种表示方式：

  • 自然语言
  1. 记录最左边索引 low 为 0，最右边索引 high 为 1023
  2. 设置 mid 为 low 和 high 的中间值
  3. 比较 numbers[mid]与 target
  4. 如果 target 大，将 low 设为 mid + 1
  5. 如果 target 小，将 high 设为 mid - 1
  6. 回到第 2 步，直到 low 大于 high
  7. 输出在不在的结果

  • 流程图

  • 算法可视化

线性搜索与二分搜索算法可视化

  • 程序语言
python
#求lis中第一个大于等于target的索引
def bs(lis,target):
    l,r = 0, len(lis)-1
    while l <= r:
        mid = (l + r)//2
        if lis[mid] < target:
            l = mid + 1
        else:
            r = mid - 1
    return l

总结 ​

接下来，我们随机生成一个数 target，在 0~10**6 的有序数列中寻找这个数是否存在。

下面就是二分搜索与线性搜索的代码运行对比！

可以发现，线性搜索的代码运行时间要超过二分搜索。（可以多运行几次，比较平均时间）

二分搜索

python
import random
def bs(lis,target):
    l,r = 0, len(lis)-1
    while l <= r:
        mid = (l + r)//2
        if lis[mid] < target:
            l = mid + 1
        else:
            r = mid - 1
    return l

numbers = [i for i in range(10**6)]
target = int(random.random()*10**7)
l,r = 0,10**6-1
if bs(numbers, target) == target:
    print(target, 'In')
else:
    print(target, 'Not in')

线性搜索

python
import random
def ls(numbers,target):
    for i in numbers:
      if target == i:
          return True
    return False
numbers = [i for i in range(10**6)]
target = int(random.random()*10**7)
if ls(numbers,target):
    print(target, 'In')
else:
    print(target, 'Not in')

二分搜索与线性搜索的时间复杂度则相差很大，假设 numbers 的长度为 n。

  • 线性搜索的平均运行次数是 n，记为 O(n)。
  • 而二分搜索的平均运行次数是 log2n，记为 O(logn)。

二分搜索与线性搜索的空间复杂度应该是一样的，假设 numbers 的长度为 n，都只用到了 n 量级的空间，所以都记为 O(n)。

线性搜索二分搜索
时间复杂度O(n)O(logn)
空间复杂度O(n)O(n)

练习 ​